0x00 介绍
该博客是我经过几个博客的讲解 在加上自己在理解这个算法时的一点坑总结的 应该对大家KMP了解有个很大帮助 下面讲解把主串都写为str,模式匹配串为ptr
KMP是三位大牛:D.E.Knuth、J.H.Morris和V.R.Pratt同时发现的。其中第一位就是《计算机程序设计艺术》的作者!!
KMP算法要解决的问题就是在字符串(也叫主串)中的模式(pattern)定位问题。说简单点就是我们平时常说的关键字搜索。模式串就是关键字,如果它在一个主串中出现,就返回它的具体位置,否则返回-1(常用手段)0x01 讲解
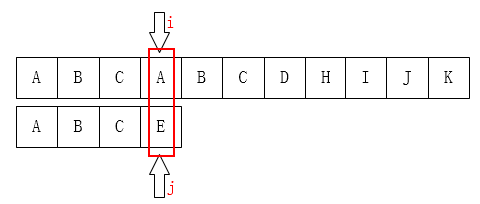
像如图一样 如果匹配到最后一个不一样的话 按照普通的字符串匹配BF算法 需要从主串的第二个开始匹配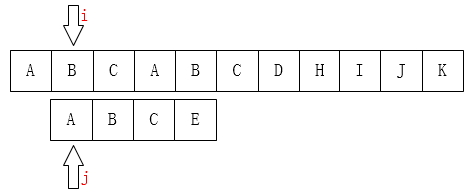
会发现为何不跳过主串的BC直接从A比较 因为匹配肯定要从主串的A开始才可以继续向后匹配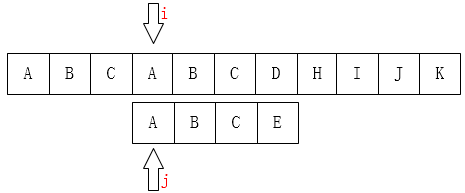
这虽是一个很节省的办法 可是给大家看另外一个例子1
2
3
4
5
6
7
8str:
+---------------------+
|S|S|S|S|S|S|S|S|S|S|A|
+---------------------+
ptr:
+-------------+
|S|S|S|S|S|S|B|
+-------------+
我们会发现如果去str上找与ptr第一个字符相同的再去比较会发现 全都是S 还需要一个一个比较 那有没有把所有情况都综合在一起的最优匹配法
那就是KMP算法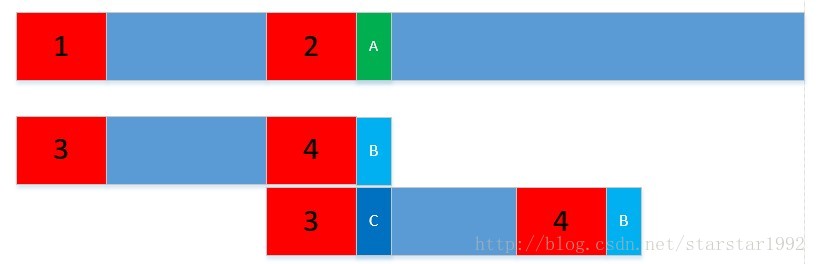
如该图(1 2 3 4是相同的字符串 并且把1 3称为前缀 2 4为后缀) 下面主串与匹配串匹配到4(也就是主串是2的地方)的后面B和A是不相同的 可以把匹配串的头也就是3移动到4的位置(也就是和2对应位置)开始继续匹配 主串就不需要从1开始向后一一匹配
可能现在讲 一下子不太懂 接着看
如图(把主串黑色框带1号区域 红色为2号区域 模式匹配串黑色为3号区域 红色为4号区域 方便说明)
当主串与模式匹配串匹配到d和c时候不相同 模式匹配串可以直接移动3号区域与原来自己的4号区域对齐 再继续匹配 为什么呢?
因为原先的模式匹配串4区域与字串的2区域是相同的4又与3是一样的 就表示在1 2之间没有与3匹配的1
2
3
4
5
6
7
8
9+---------------------+
|s|a|b|t|a|a|b|t|d|c|a|c|
|a|b|t|a|a|b|n|
+-----------+
+---------------------+
|s|a|b|t|a|a|b|t|d|c|a|c|
|a|b|t|a|a|b|n|
+-----------+
注意最长前缀:是说以第一个字符开始,但是不包含最后一个字符。 最长后缀一样的道理
如上 当模式匹配串匹配到n与t时候不一样 并且n前面的字符串有相同的前缀和后缀(ab)
如果模式匹配串的后缀开始匹配不同(就是模式匹配串后面的ab开始的匹配) 就可以从模式匹配串前缀开始 去进行原先后缀没有匹配成功的哪里去匹配 不必要从前缀和后缀之间去一个一个匹配 因为相对的主串之间不可能存在与模式匹配串前缀相同的字符串 如上图模式匹配串中虽然存在与模式匹配串第一个字符相同的a 并且有两个 如果按照之前的移动到主串下一个a的地方会发现第一个
a后面的ab自然与主串中不匹配 但是如果移动到第二个a(即移动到原先后缀的地方) 会发现可以省去前面字符的匹配 我写的这个模式匹配串前缀ab和后缀ab之前只有一个a 万一中间有很多字符
那在中间匹配就很浪费时间 这样的kmp算法 就能节省很多时间
用简单明了的句子去说就是模式匹配串如果匹配到某个位置与主串不一样的话 判断模式匹配串该位置前面的字符串是否是相同的最长前缀和最长后缀(如abtab,ababa) 这里一定要好好理解! 自己那笔写几个例子
下面的问题就是 如何知道我匹配到不成功的时候前面是不是有相同的最长前缀和最长后缀 如何前缀移动到原先后缀处 而大牛们就想了个办法 先用一个next[]数组去存模式匹配串从头开始的所
有字串 还看上面的例子1
2
3
4
5
6
7
8
9+---------------------+
|s|a|b|t|a|a|b|t|d|c|a|c|
|a|b|t|a|a|b|n|
+-----------+
+---------------------+
|s|a|b|t|a|a|b|t|d|c|a|c|
|a|b|t|a|a|b|n|
+-------------+
模式匹配串后缀ab中的b是字符串的第5个位置 那我们就想办法让next[5]存的是相同前缀ab中b的位置就可以! 这样当判断到后缀后的字符不匹配时就可以通过next[]去移动到前缀1
2while(ptr[k+1] != str[i])
k = next[k];
看这个代码ptr是模式匹配字符串 str是主串 i是匹配到主串的那个位置 k是后缀最后一个字符的位置 k+1就是后缀后第一个字符开始去与主串匹配 如果不同就代表后缀开始的匹配不成功
从而k = next[k] 移动到前缀的b位置 所以此时的next[5] = 1 因为abtaab的前缀b为ptr[1],(数组从0开始) 那相同的ababa如果后缀aba后的字符匹配不相同时所有后缀的最后一个字符
next[4] = 2 会发现next存的就是相同的前缀和后缀的最大长度-11
2
3
4
5
6对于目标字符串ptr,ababaca,长度是7,
所以next[0],next[1],next[2],next[3],next[4],next[5],next[6]分别计算的是
a,ab,aba,abab,ababa,ababac,ababaca的相同的最长前缀和最长后缀的长度
由于a,ab,aba,abab,ababa,ababac,ababaca的相同的最长前缀和最长后缀是“”,“”,“a”,“ab”,“aba”,“”,“a”
所以next数组的值是[-1,-1,0,1,2,-1,0]
这里-1表示不存在,0表示存在长度为1,2表示存在长度为3。这是为了和代码相对应。
而KMP比较难也比较复杂的就是这个next数组的构造1
2
3
4
5
6
7
8
9
10
11
12
13void Createnext(char *ptr, int *next, int psize) //传入参数模式匹配字符串 next数组 模式匹配字符串长度
{
int k = -1;
next[0] = -1; //next[0]必为-1
for(int i=1;i<psize;i++)
{
while(k>-1 && ptr[k+1]!=ptr[i]) //如果不匹配 k = next[k]
k = next[k];
if(ptr[k+1] == ptr[i])
k = k+1; //如果相同k+1
next[i] = k; //-1表示不存在,0表示存在长度为1,2表示存在长度为3。这是为了和代码相对应
}
}
这个for循环就是计算next[0],next[1],…next[q]…的值。
比如我们已经知道ababab,q=4时,next[4]=2(k=2,表示该字符串的前5个字母组成的子串ababa存在相同的最长前缀和最长后缀的长度是3,所以k=2,next[4]=2。这个结果可以理解成我们自己观察算的,也可以理解成程序自己算的,这不是重点,重点是程序根据目前的结果怎么算next[5]的).,那么对于字符串ababab,我们计算next[5]的时候,此时q=5, k=2(上一步循环结束后的结果)。那么我们需要比较的是str[k+1]和str[q]是否相等,其实就是str[1]和str[5]是否相等!,为啥从k+1比较呢,因为上一次循环中,我们已经保证了str[k]和str[q](注意这个q是上次循环的q)是相等的(这句话自己想想,很容易理解),所以到本次循环,我们直接比较str[k+1]和str[q]是否相等(这个q是本次循环的q)。
如果相等,那么跳出while(),进入if(),k=k+1,接着next[q]=k。即对于ababab,我们会得出next[5]=3。 这是程序自己算的,和我们观察的是一样的。
如果不等,我们可以用”ababac“描述这种情况。 不等,进入while()里面,进行k=next[k],这句话是说,在str[k + 1] != str[q]的情况下,我们往前找一个k,使str[k + 1]==str[q],是往前一个一个找呢,还是有更快的找法呢? 程序给出了一种更快的找法,那就是 k = next[k]。 程序的意思是说,一旦str[k + 1] != str[q],即在后缀里面找不到时,我是可以直接跳过中间一段,跑到前缀里面找,next[k]就是相同的最长前缀和最长后缀的长度。所以,k=next[k]就变成,k=next[2],即k=0。此时再比较str[0+1]和str[5]是否相等,不等,则k=next[0]=-1。跳出循环。
如果还不理解while是干嘛的话 我再举例子 当模式匹配串abcabtmnabcabcmn 构造next数组到abcabtmnabcabc字串的时候 k就是前缀abcab的最后一个b的位置 当判断k+1(也就是吧后面t)与i
(也是现在匹配的最后一个c)不同时候(t与c不同) 就会发生k = next[k] 也就是从第一个ab的后开始去与c匹配 因为abcab是拥有相同的前缀和后缀(ab) next[4]=1 也就是现在前缀b在该字符串中的位置发发现abc和后面abc是一样的 也就是abcabtmnabcabc字串的next[] = 2 这样能减少因为找与前缀相同的开头而去不停向前移动的次数
KMP代码1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16int KMP(char *str, char *ptr,int ssize, int psize)
{
int *next = new int[psize];
Createnext(ptr,next,psize);
int k = -1;
for(int i=0;i<ssize;i++)
{
while(k>-1 && ptr[k+1] != str[i])
k = next[k]; //如果没用匹配成功通过next[] 去进行移动
if(ptr[k+1] == str[i])
k = k+1; //主串去模式匹配串匹配成功过的话就+1
if(k == psize-1)
return i-psize+1; // k == psize-1时候就是匹配到模式匹配串最后 匹配成功 返回主串开始匹配的位置
}
return -1; //循环出来也没有匹配到 没有匹配的 赋值-1
}
最后的测试1
2
3
4
5
6
7
8
9
10
11int main()
{
int result = KMP("cccaba", "aba", 6, 3);
cout<<result+1<<endl;
return 0;
}
结果如下:
4 Process returned 0 (0x0) execution time : 0.159 s
Press any key to continue.
至此OVER 如果我觉得哪里没有将清楚 或者有不明白 联系我 我会帮您解决问题!
资料来源:
https://blog.csdn.net/starstar1992/article/details/54913261
https://www.cnblogs.com/yjiyjige/p/3263858.html